카이제곱검정
-교차분석이라고도 불림.
-두 범주형 변수에서 관찰된 빈도가 기대 빈도와 의미 있게 다른지를 검증하기 위해 사용된다. 즉, 두 범주형 변수 A, B가 종속사건인지 독립사건인지 판별하는 것
-자료가 빈도로 주어졌을 때, 특히 명목척도 자료의 분석에 이용됨
주의사항
-자유도가 1일 경우 각 관측값이 30 이상이어야 한다.
카이제곱값 계산 공식:
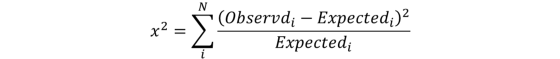
(예시)
1) 가설 세우기
귀무가설 H0 : 성별과 쿠폰 간 상관성이 없다.
대립가설 H1 : 성별과 쿠폰 간 상관성이 있다.
2) 관측도수
| 쿠폰 반응 | 쿠폰 미반응 | total | |
| 남성 | 200 | 300 | 500 |
| 여성 | 220 | 260 | 480 |
| total | 420 | 560 | 980 |
3) 기대도수 구하기
| 쿠폰 반응 | 쿠폰 미반응 | total | |
| 남성 | 214.29 | 285.71 | 500 |
| 여성 | 205.71 | 274.29 | 480 |
| total | 420 | 560 | 980 |
4) 범주별 카이제곱값 구하기
| 쿠폰 반응 | 쿠폰 미반응 | total | |
| 남성 | 0.952381 | 0.714286 | 1.666667 |
| 여성 | 0.992063 | 0.744048 | 1.736111 |
| total | 1.944444 | 1.458333 | 3.402778 |
5) 전체 카이제곱값 구하기
= 3.402778
6) 자유도 구하기
= (2-1) * (2-1) = 1
7) 검정
유의수준 5%의 카이제곱값은 3.84
우리의 카이제곱값은 3.402778 < 3.84
따라서 귀무가설을 기각할 수 없다.
즉, 성별과 쿠폰 반응간 상관성이 없다.

참고문헌
https://hsm-edu.tistory.com/1366
카이제곱검정 예시 모음 (2수준)
카이제곱검정은 집단들의 비율을 비교하는 검정입니다. 일반적으로 두 집단의 비율 비교에 주로 사용하며 세 집단 이상 비교할 경우 사후검정을 해야 어느 집단 사이에 차이가 있는지 알 수 있
hsm-edu.tistory.com
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=narasemi&logNo=221396627086
[통계 상식] 카이제곱 검정
안녕하세요~ 나라세미입니다! 오늘 배워 볼 통계 상식은 카이제곱 검정입니다~ ① 카이제곱 검정이란? (두 ...
blog.naver.com
https://partrita.github.io/posts/thinkstat2/
파이썬으로 배우는 통계학
0. 통계적 사고¶아래 내용은 통계적 사고: 파이썬을 이용한 탐색적 자료 분석 을 읽고 내용을 정리한 것이다. 이 책의 원제는 Thinkstat2(저자 Allen B. Downey) 로 저자는 올린공대 컴퓨터과학과의 교수
partrita.github.io
https://hsm-edu.tistory.com/1214
비율검정과 카이제곱검정은 같은가 다른가
비율검정과 카이제곱검정을 두고 헷갈려 하시는 분들이 계실거라 생각됩니다. 뭔가 비슷한 것 같기도 한데 막상 구분해서 설명하자니 어려운 그런 혼란을 저도 겪었습니다. 오늘은 그 애매함을
hsm-edu.tistory.com
https://liujingjun.tistory.com/81
카이제곱검정
웹 테스트 시, 종종 단순한 A/B 검정을 넘어 동시에 여러 가지 처리를 한 번에 테스트할 필요가 있다. 카이제곱검정은 횟수 관련 데이터에 주로 사용되며 예상되는 분포에 얼마나 잘 맞는지를 검
liujingjun.tistory.com
https://warm-uk.tistory.com/28
[통계기초] 통계분석 : 가설검정 : 카이제곱(적합도, 독립성, 분산, 분산비)
* 자료출저 및 참고강의 패스트캠퍼스 올인원 패키지(금융공학/퀀트) 장순용 강사님 인터넷 강의 * 목차 통계분석 : 가설검정 : 카이제곱(적합도, 독립성, 분산, 분산비) 핵심) 1. 카이제곱 확률분
warm-uk.tistory.com
http://www.statedu.com/?mid=QnA&comment_srl=78451&page=501&document_srl=78734
통계분석 Q & A - [re] 카이스퀘어 검정에 관한 질문
지금 질문하신 내용이 카이스퀘어 검정의 결정적인 맹점입니다. 즉, 비율은 같다 하더라도, 전체 case의 수가 커지면 카이제곱 값은 커지게 됩니다. 그 이유는 %를 이용하여 계산하는 것이 아니라
www.statedu.com
'Artificial Intelligence' 카테고리의 다른 글
| [Pytorch] model.eval()과 with torch.no_grad()의 차이점 (0) | 2023.04.20 |
|---|---|
| 책 "BERT와 GPT로 배우는 자연어 처리" 후기 - 한국어 언어모델 입문서적으로 최고인 책 (0) | 2022.01.10 |
| 척도의 종류와 의미 (0) | 2021.08.16 |
| 히스토그램의 정의, 장단점 (0) | 2021.08.09 |
| 빅데이터 시스템 조직 및 운영 체계 (1) | 2021.04.14 |

